A body is not made up of a single particle instead it is a collection of large number of particles arranged in a particular way. Here we find a point in a system of a collection of particles that behaves as the centre of the combination of the total mass of all particles which is called centre of mass of the system of particles.
A rigid body can be taken as a collection of particles. Here we find the centre of mass of a rigid body. A net force acts on a rigid body as shown in Figure 1. The body is made up of a large number of particles of masses \(m_1\), \(m_2\), \(m_3\) etc..
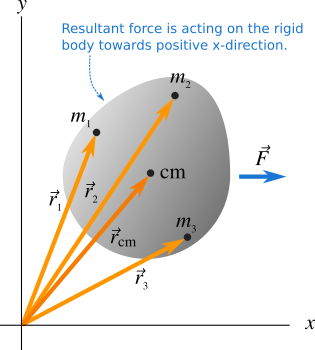
The position vector of mass \(m_1\) is \(\vec r_1\), and that of mass \(m_2\) is \(\vec r_2\) and so on. The body undergoes a displacement towards positive x-direction under the action of a net force \(\vec F\). The total resultant force on the body is the sum of the forces on individual particles. The force on a particle of mass \(m_1\) is \(\vec F_1\) and on a particle of mass \(m_2\) is \(\vec F_2\), therefore we can represent the force on any particle of mass \(m_i\) as \(\vec F_i\) and the total resultant force is the sum of the forces on all particles of the body. Hence we can write,
\[\begin{align*} {\vec F _{{\rm{res}}}} &= \sum\limits_{i = 1}^n {{{\vec F }_i}} \\ {\rm{or}}\quad M{\vec a _x} &= \sum\limits_{i = 1}^n {{m_i}{{\vec a }_i}} \\ {\rm{or}}\quad M\frac{{{d^2}\vec r }}{{d{t^2}}} &= \sum\limits_{i = 1}^n {{m_i}\frac{{{d^2}{{\vec r }_i}}}{{dt}}} \\ {\rm{or}}\quad \frac{{{d^2}\vec r }}{{d{t^2}}} &= \frac{{{d^2}}}{{d{t^2}}}\left( {\frac{{\sum\limits_{i = 1}^n {{m_i}{{\vec r }_i}} }}{M}} \right)\\ {\rm{or}}\quad \vec r &= \frac{{\sum\limits_{i = 1}^n {{m_i}{{\vec r }_i}} }}{M} \tag{1} \label{1} \end{align*}\]
The acceleration vector is the double derivative of the position vector. The position vector given by Equation \eqref{1} is the position vector of the centre of mass of the rigid body. Which can be rewritten as \(\vec r_{\text{cm}}\) where the subscript "\(\text{cm}\)" represents centre of mass. The total mass \(M\) of the rigid body is the sum of all masses of individual particles, so \(M = \sum\limits_{i = 1}^n {{m_i}} \) and
\[{{\vec r}_{{\rm{cm}}}} = \frac{{\sum\limits_{i = 1}^n {{m_i}{{\vec r}_i}} }}{{\sum\limits_{i = 1}^n {{m_i}} }} \tag{2} \label{2}\]
The position vector \(\vec r_{\text{cm}}\) can be written in component form as \({\vec r _{{\rm{cm}}}} = {x_{{\rm{cm}}}}\hat i + {y_{{\rm{cm}}}}\hat j + {z_{{\rm{cm}}}}\hat k\) where \({x_{{\rm{cm}}}}\), \({y_{{\rm{cm}}}}\) and \({z_{{\rm{cm}}}}\) are the x, y and z-coordinates of the centre of mass respectively. And similarly the position vector of any particle in component form is \({\vec r _{{\rm{i}}}} = {x_{{\rm{i}}}}\hat i + {y_{{\rm{i}}}}\hat j + {z_{{\rm{i}}}}\hat k\). So,
\[\begin{align*} {{\vec r}_{{\rm{cm}}}} &= \frac{{\sum\limits_{i = 1}^n {{m_i}{{\vec r}_i}} }}{{\sum\limits_{i = 1}^n {{m_i}} }}\\ &= \frac{{\sum\limits_{i = 1}^n {{m_i}({x_{\rm{i}}}\hat i + {y_{\rm{i}}}\hat j + {z_{\rm{i}}}\hat k)} }}{{\sum\limits_{i = 1}^n {{m_i}} }}\\ &= \frac{{\sum\limits_{i = 1}^n {{m_i}{x_{\rm{i}}}\hat i + \sum\limits_{i = 1}^n {{m_i}{y_{\rm{i}}}\hat j} + \sum\limits_{i = 1}^n {{m_i}{z_{\rm{i}}}} \widehat k} }}{{\sum\limits_{i = 1}^n {{m_i}} }} \tag{3} \label{3} \end{align*}\]
Now after comparing Equation \eqref{3} with \({\vec r _{{\rm{cm}}}} = {x_{{\rm{cm}}}}\hat i + {y_{{\rm{cm}}}}\hat j + {z_{{\rm{cm}}}}\hat k\), we'll get
\[{x_{{\rm{cm}}}} = \frac{{\sum\limits_{i = 1}^n {{m_i}{x_{\rm{i}}}} }}{{\sum\limits_{i = 1}^n {{m_i}} }} = \frac{{{m_1}{x_1} + {m_2}{x_2} + {m_3}{x_3} + ... + {m_n}{x_n}}}{{{m_1} + {m_2} + {m_3} + ... + {m_n}}}\]
\[{y_{{\rm{cm}}}} = \frac{{\sum\limits_{i = 1}^n {{m_i}{y_{\rm{i}}}} }}{{\sum\limits_{i = 1}^n {{m_i}} }} = \frac{{{m_1}{y_1} + {m_2}{y_2} + {m_3}{y_3} + ... + {m_n}{y_n}}}{{{m_1} + {m_2} + {m_3} + ... + {m_n}}}\]
\[{z_{{\rm{cm}}}} = \frac{{\sum\limits_{i = 1}^n {{m_i}{z_{\rm{i}}}} }}{{\sum\limits_{i = 1}^n {{m_i}} }} = \frac{{{m_1}{z_1} + {m_2}{z_2} + {m_3}{z_3} + ... + {m_n}{z_n}}}{{{m_1} + {m_2} + {m_3} + ... + {m_n}}}\]
The components of the velocity of the center of mass are \(v_\text{cm-x} = dx_\text{cm}/dt\), \(v_\text{cm-y} = dy_\text{cm}/dt\) and \(v_\text{cm-z} = dz_\text{cm}/dt\). The velocity of the center of mass is \(\vec v_\text{cm} = d\vec r_\text{cm}/dt\) which is
\[\vec v_\text{cm} = \frac{m_1\vec v_1 + m_2\vec v_2 + m_3\vec v_3 + ...}{m_1 + m_2 + m3 + ...} \]
The total mass of the rigid body is the sum of the masses of individual particles which is \(M = m_1 + m_2 + m_3+ ...\) and therefore, momentum of the entire collection of particles is \(M\vec v_\text{cm} = m_1\vec v_1 + m_2\vec v_2 + m3\vec v_3 + ...\). The total momentum of the rigid body is the sum of the momenta of all particles of the rigid body and it is equal to the total mass times the velocity of the center of mass.





