Electric flux means electric field lines passing perpendicularly through a particular surface. It means we only calculate the perpendicular component of electric field passing through a particular surface to calculate electric flux. We calculate the electric flux through a surface shown in Figure 1 with uniform electric field \(\vec E\).

Figure 1(a) Electric filed through a surface of area \(A\).
Figure 1(b) The electric field lines make angle \(\theta\) with the area vector \(\vec A\).
Figure 1 Electric field lines through a surface area.

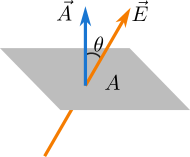
The electric flux is the perpendicular component of electric field through the area \(A\). The electric field lines make angle \(\theta\) with the area vector \(\vec A\) and therefore the component of electric field perpendicular to the area (parallel to \(\vec A\)) is \(E_\bot = E \cos \theta\). Therefore the electric flux denoted by \(\Phi\) is

\[\Phi = AE\cos \theta \tag{1} \label{1}\]

If the electric field is not uniform, it's the time to divide the area \(A\) into infinitesimal area elements \(dA\). The electric field is uniform through the area \(dA\) and the electric flux through this area is \(d\Phi = dAE \cos \theta\). Therefore we integrate to find the total electric flux through the area \(A\).

\[\Phi = \int {E\cos \theta {\kern 1pt} dA} \tag{2} \label{2}\]

Figure 2 The electric field lines entering the closed surface must come out of the surface. Therefore the net electric flux through the surface is zero.

In case of the charge outside the closed surface, the electric flux through the closed surface is always zero. The electric field lines entering a closed surface must come out of the surface and the net electric flux is zero. The Figure 2 shows that the electric field lines entering the closed surface also come out of the surface and the net electric flux is through the closed surface is zero.